프로그래밍에서 정수가 2의 N제곱꼴인지 판별하기

2의 N제곱꼴은 소인수로 2만을 가진다는 특징이 있습니다(그것이 2의 N제곱이니까...)

 

 

그러므로 다음과 같이 판별이 가능합니다.

 

1. (기저사례) 일단, 0 이하의 정수는 2의 제곱꼴이 아니므로 제외합니다.
2. 2로 나누어 떨어지는지 검사하고 만약 나누어 떨어진다면 2로 나누어 줍니다.
3. 더 이상 나누어 떨어지지 않을 때까지 위 과정을 반복합니다.
4. 최종 결과가 1이라면 2의 N제곱, 1이 아니라면 2의 N제곱이 아닙니다.

코드로는 다음과 같이 작성이 가능합니다.

fun isPowerOf2(n: Int): Boolean {
	if (n <= 0) {
		return false
	}

	var num = n
	while (num % 2 == 0) {
		num /= 2
	}

	return num == 1
}

fun main(args: Array<String>) {
	(0..100).forEach {
		if (isPowerOf2(it)) {
			println("$it is power of 2")
		}
	}
}

실행 결과는 다음과 같습니다.

 

 

이제 시간복잡도를 생각해봅시다. 2로 나누어 떨어지지 않을 때까지 계속해서 2로 나누므로 대략 log2(N)번 연산함을 알 수 있고, 빅오표기법으로 나타내면 O(log N)이 됩니다.

 

더 빠르게 구할 수도 있을까요?

 

2의 N제곱은 이진수로 나타내면 1, 10, 100, 1000, ... 꼴이 됩니다. 여기서 각 수에 1을 빼면 0, 01, 011, 0111, ... 꼴이 됩니다.

이 둘을 비트 &를 해주면 그 결과는 모두 0이 됩니다!!

 

1 & 0              --> 0

10 & 01          --> 0

100 & 011      --> 0

1000 & 0111  --> 0

 

따라서 2의 N제곱꼴인지의 판단은 다음과 같이 할 수도 있습니다.

fun isPowerOf2(n: Int): Boolean {
	return n > 0 && (n and (n - 1)) == 0
}

이렇게 작성하면 시간복잡도는 O(1)이 됩니다.

 

 

 

번외 - 3의 N제곱꼴 판단하기

3의 N제곱꼴은 이진수로 나타내면 1, 11, 1001, 11011, ... 꼴이 되고 딱히 규칙을 찾을 수 없습니다.

이 경우엔 어쩔 수 없이 O(log N)으로 작성해야 할까요?

 

놀랍게도 3의 N제곱꼴도 O(1)로 판단하는 것이 가능합니다.

(한번 고민해보시고, 아래 글을 펼쳐보세요)

 

보통 프로그래밍 언어에서 사용하는 정수형은 32비트 또는 64비트라는 성질을 이용하는 방법이 있습니다.

(파이썬처럼 기본 빅인티져 제외)

 

32비트의 경우 범위 내에서 가장 큰 3의 제곱수는 3의 19제곱(=11억 6226만 1467)입니다. 단, unsigned 자료형이라면 3의 20제곱(=34억 8678만 4401)입니다.

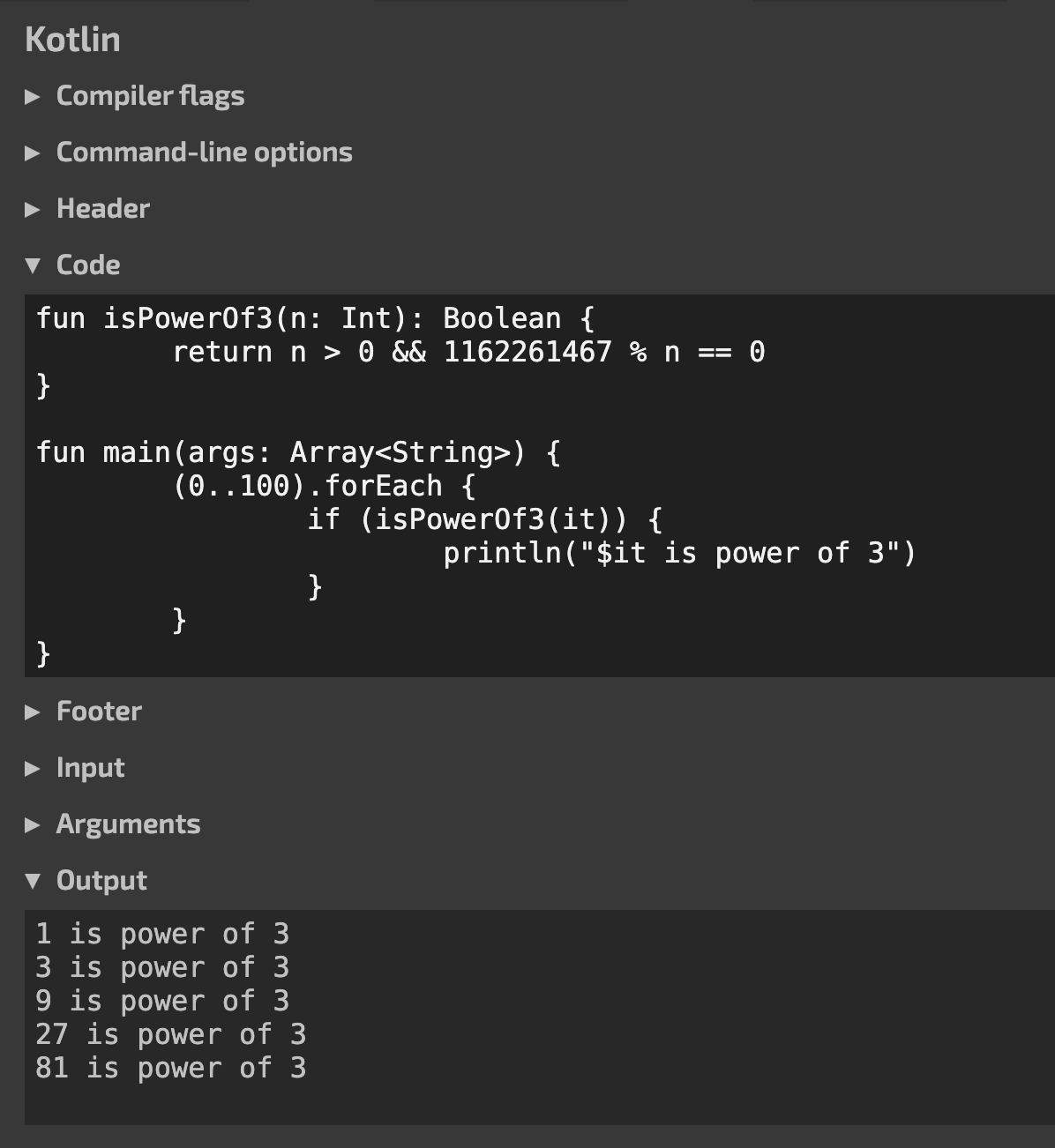
따라서 다음처럼 작성하면 O(1)로 3의 N제곱꼴인지 판단하는 것이 가능합니다.

 

fun isPowerOf3(n: Int): Boolean {
	return n > 0 && 1162261467 % n == 0
}